다 같이 즐거운 명제 놀이를 해보자.
우선 미니언은 잡을 줄 알아야 하니 여러분들에게 기본기(평타)를 알려드리겠다.
평타 1 [모든]
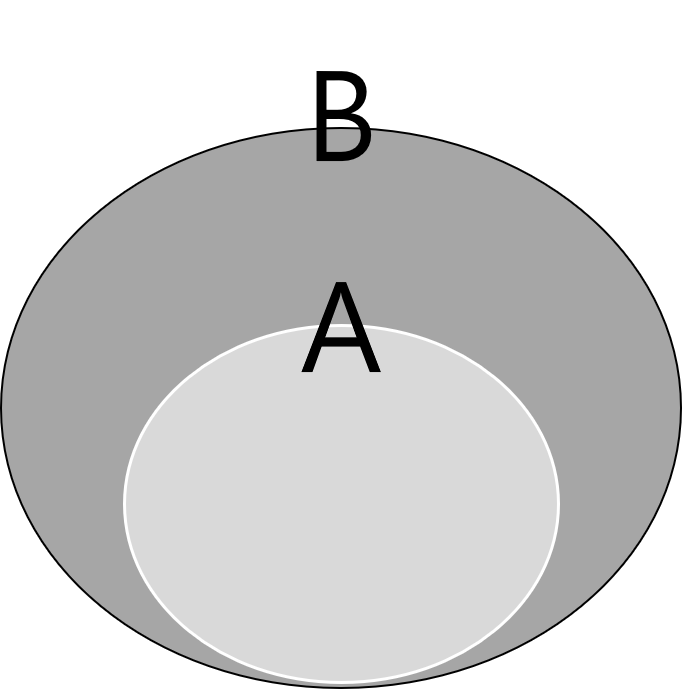
명제 1) 모든 A는 B이다.
이처럼 '모든'으로 묶여있고 '는'이라는 단어 사이에 포함관계가 왼쪽에서 오른쪽으로 성립한다.
즉, 'A⊂B'가 성립한다. 또한 A는 B와 동일 관계일 수 있다. 'A=B'도 된다.
여기서 '모든'은 생략되어도 같은 의미를 지닌다. (=A는 B이다.)

다들 알겠지만 명제가 참일 경우 대우 명제도 참이다.
따라서 명제 1의 대우 명제 < 모든 B가 아닌 것은 A가 아니다. > 역시 성립한다.
평타 2 [어떤]
명제 2) 어떤 C는 D이다.
'어떤'은 C의 일부분이 D의 일부분이라는 의미이다. 즉, C∩D≠Ø. C와 D는 교집합이 존재한다.
또한 '어떤'은 '대우'가 성립하지 않고 '역'이 성립한다.

요약하자면, '모든'은 포함관계, '어떤'은 교집합을 생각하자.
평타를 알려드렸으니 스킬을 알려드리겠다.

[난이도:★☆☆☆☆] 모모모 (삼단논법)
전제 ) 모든 1은 2이다.
전제 ) 모든 2는 3이다.
---------------------------
결론 ) 모든 1은 3이다.
예시) 모든 사람은 죽는다. 소크라테스는 사람이다.
그러므로 소크라테스는 죽는다.
깔끔하쥬?

[난이도: ★★☆☆☆] 모모어
전제 ) 모든 1은 2이다.
전제 ) 모든 1은 3이다.
---------------------------
결론 ) 어떤 2는 3이다.
아니 갑자기 '어떤'이 왜 튀어나오는 건가! 할 수 있지만 벤다이어그램을 그리면 맞긴 맞네하고 인정할 수밖에 없어버리기...
예시 ) 모든 헬창은 무게충이다. 모든 헬창은 자극충이다.
어떤 무게충은 자극충이다. (사실 진리)

[난이도: ★★★☆☆] 어모어
전제 ) 어떤 1은 2이다.
전제 ) 모든 2는 3이다.
---------------------------
결론 ) 어떤 1은 3이다.
예시) 어떤 옷은 명품이다. 모든 명품은 비싸다.
어떤 옷은 비싸다.
이제 실전 연습을 한번 해보자.
제가 만든 문제라 똥망일 수도 있지만, 난이도는 중상?

정답은 5 <-여길 드래그하세요.
자 이제 딜레마를 맞이할 준비가 되셨습니다.
| 추리 1 | 추리 2 |
|
모든 대학생은 취준생이다. 어떤 취준생은 대기업을 좋아한다.
so, 어떤 대학생은 대기업을 좋아한다. |
어떤 대학생은 취준생이다. 모든 취준생은 대기업을 좋아한다. so, 어떤 대학생은 대기업을 좋아한다. |
추리 1
일반적인 공식. 즉 어모어 스킬로 풀어보자.
모든 대학생은 취준생이다.
모든 a -> b
어떤 취준생은 대기업을 좋아한다.
어떤 b -> c
so, 어떤 대학생은 대기업을 좋아한다.
so, 어떤 a -> c
모두들 a에서 시작하여 Z 모양으로 시선이 이동할 것이다. 짝짝짝~
그럼 문제의 추리 2를 알아보자.
어떤 대학생은 취준생이다.
어떤 a -> b
모든 취준생은 대기업을 좋아한다.
모든 b -> c
so, 어떤 대학생은 대기업을 좋아한다.
so, 어떤 a -> c
모두들 a에서 시작하여 Z 모양으로 시선이 이동할 것이다22. 짝짝짝222~
.............. 응???? 나만 자연스러워요?
멘붕. 몇 번을 봐도 같은 결과가 나옵니다. 너무 자연스러워요.
이제부터 오늘의 깨달음입니다.

어떤 A B
모든 B C
는 성립

모든 A B
어떤 B C
는 안됩니다.
벤다이어그램으로 확인하면 분명하다. 어모어는 성립하지만 모어어는 성립하지 않는다. 혹시나 해서 하는 말이지만 우리는 맞는 것보다 아닐 수 있는 게 중요하다. 즉, 반례가 있는지가 중요한 것이다.
끝.
'공부' 카테고리의 다른 글
| 명제놀이 질문 답변 (0) | 2021.02.10 |
|---|---|
| gsat 언어추리 (0) | 2020.06.12 |
